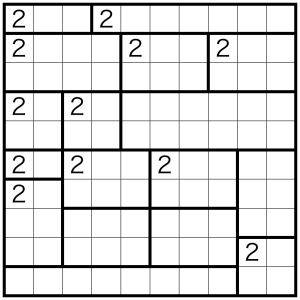
It’s always fun to figure out some new arguments in a puzzle type. While going through @taburega’s tough puzzles, I ran into one occurrence of a pattern I didn’t know before, and recently managed to distill it into something a bit more memorable while finding some similar arguments in a kwontomloop.com puzzle.
I’m curious how well known these techniques are, let me know! I hope to follow this up with a discussion of the “theory” at some point.
Rules This is a Slitherlink puzzles with many solutions, all of which share one segment. Find that segment.