Here’s a pair of practice puzzles for the upcoming Bulgarian GP.
Rules Solve as a regular skyscrapers puzzle. In addition, all even clues are given. (That is, any missing clues would be odd numbers if given.)
Here’s a puzzle from my preparation for WPC 2019 that I don’t believe I’ve posted yet. It’s also sort of a practice puzzle for the upcoming first round of the 2020 Puzzle GP, which features the variant Terra XX.
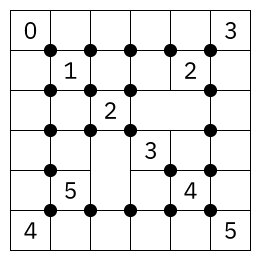
Rules Place numbers in the empty cells, from the range 0-9. Same numbers can’t be adjacent (but may touch by a corner). Wherever four cells meet at a vertex (marked by a black dot), the sum of the numbers in those cells must be 10.
We continue with the regular puzzle-a-month-on-the-first-of. Here’s a Skyscraper-Nurikabe, a practice puzzle for the upcoming Indian GP.
Rules Solve as a regular Nurikabe. Additionally, some skyscraper clues are given outside the grid. For these, consider the blocks of adjacent shaded cells within the corresponding row as skyscrapers with height equal to the number of cells in the block.
Or check the instruction booklet which includes an example.
You can solve online (of sorts) and check your code here.
Just a tiny puzzle that I made as an example for the croco WPC preparation series. It was a bit too hard as an example; the type seems inherently hard.
Rules Place some lamps in the empty cells around the grid, with brightness 0 to 3. The lamps shine horizontally, vertically and diagonally in eight directions. In each direction, they illuminate as many cells as they are bright. Numbers inside the grid indicate how many lamps illuminate the corresponding cell.
The WPC instruction booklet has an example.
The next round of the Puzzle GP takes place next weekend, with the Dutch round authored by Bram de Laat. The instructions are out; it turns out Maxi Loop is one of the types (see Puzzle 91 and Puzzle 109), so we’ve got that done. One of the less familiar types is Greater Wall, compare Bram’s set for the Polish championships. The presentation has been much improved, with explicit placeholders. Here’s one.
Rules Shade some cells to form a wall that is connected by edge and doesn’t contain any 2×2-square. Where given, clues outside indicate all connected blocks of shaded cells in the corresponding row or column, in the correct order. Relations between two placeholders apply to the lengths of the corresponding blocks.
One more Tom-tom puzzle. That’s it for the series.
Rules Fill the grid with digits 1-7, so that no digit repeats within a row or a column. (Digits may repeat within rooms.) Clues indicate the result of applying a basic operation (addition, subtraction, multiplication, division) to the digits within that room, starting with the largest digit.
Or see the instruction booklet.
One Tom-tom puzzle.
Rules Fill the grid with digits 1-7, so that no digit repeats within a row or a column. (Digits may repeat within rooms.) Clues indicate the result of applying a basic operation (addition, subtraction, multiplication, division) to the digits within that room, starting with the largest digit.
Or see the instruction booklet.
One more Nanro Signpost.
Rules Shade some cells, so that all shaded cells are connected, and such that shaded cells don’t fill any 2×2 square. Clues indicated the number of shaded cells in an area; each area must have at least one shaded cell. Whenever two shaded cells touch across walls, the number of shaded cells within both areas must be different.
Or see the instruction booklet, with a somewhat different formulation of the rules.
One more practice puzzle, a Nanro Signpost.
Rules Shade some cells, so that all shaded cells are connected, and such that shaded cells don’t fill any 2×2 square. Clues indicated the number of shaded cells in an area; each area must have at least one shaded cell. Whenever two shaded cells touch across walls, the number of shaded cells within both areas must be different.
Or see the instruction booklet, with a somewhat different formulation of the rules.
Maybe Puzzles 