Tag Archives: tapa

Puzzle 155: Minesweeper-Tapa

Leave a reply

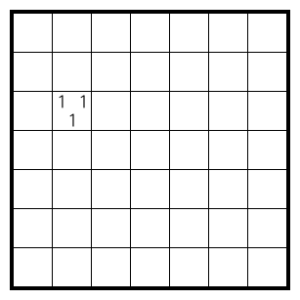
Here’s another puzzle I made in preparation for the recent Logic Masters. It’s a Minesweeper Tapa, a type from the Tapa round on the contest.

In other news, results have now been posted: https://logic-masters.de/LM/2018_e_tabelle.php. (It seems linear time bonus really isn’t the right choice where players finish after a fraction of the round: On round 6 I took 3.5 minutes compared to the next player’s 5 minutes, for a factor 1.06 in points.)

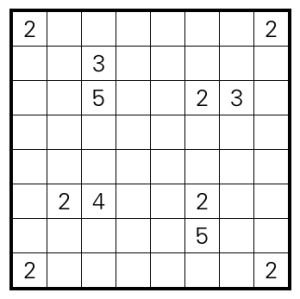Rules Solve as a regular Tapa, except the clues just specify the total number of shaded cells in the surrounding cells, as in Minesweeper.

Puzzle 93b: Regular Tapa

Leave a reply

I thought the underlying “regular” Tapa from the JaTaHoKu I published earlier was worthy of a dedicated post. Is there a name around for this variant?

While resolving this one will require a few case distinctions, it does have a reasonable break-in, and is quite doable if you choose the right spots. It’s possible that prescribing the number of shaded cells is not necessary, give it a try with three shaded cells per row/column.

tapa-regular

Rules Solve as a regular Tapa. Additionally, there must be exactly four shaded cells in every row and column.

Puzzle 98: JaTaHoKu, cryptic

Leave a reply

Last JaTaHoKu for now, a JaTaHoKu with cryptic clues. I made a triagonal one, too, but didn’t get around to rendering that yet. Maybe later.

jatahoku1-6crypt

Rules Place numbers from 1 to 6 into some empty cells, such that each row, column and region contains each number exactly once. Clues within the grid are Tapa clues; the numbered cells form a valid Tapa solution with respect to these. Clues along the bottom and right edges are skyscraper clues. Clues along the top and left are Japanese Sums clues, with question marks standing in for unspecified digits. (I.e., 10 would be two question marks.)

Some digits have been replaced by letters. Equal letters correspond to equal digits, different letters to different digits.

Puzzle 97: JaTaHoKu, cylindrical

2 Replies

Another JaTaHoKu, this time cylindrical.

jatahoku1-5cylinder

Rules Place numbers from 1 to 5 into some empty cells, such that each row, column and region contains each number exactly once. Clues within the grid are Tapa clues; the numbered cells form a valid Tapa solution with respect to these. Clues along the bottom and right edges are skyscraper clues. Clues along the top and left are Japanese Sums clues, with question marks standing in for unspecified digits. (I.e., 10 would be two question marks.)

The grid wraps around from top to bottom. Clues along the top act as Japanese Sums clues in order, starting at any group of numbers. Clues along the bottom act as Skyscraper clues, starting at 1. (So for example, a clue ‘1’ is impossible.)

Puzzle 95: JaTaHoKu

Leave a reply

Another JaTaHoKu, this one using the full rule set. It’s probably a bit easier than the first one. Note that the given 4s in the grid are Tapa clues.

jatahoku1-5

Rules Place numbers from 1 to 5 into some empty cells, such that each row, column and region contains each number exactly once. Clues within the grid are Tapa clues; the numbered cells form a valid Tapa solution with respect to these. Clues along the bottom and right edges are skyscraper clues. Clues along the top and left are Japanese Sums clues, with question marks standing in for unspecified digits. (I.e., 10 would be two question marks.)

Puzzle 94: JaTaHoKu

Leave a reply

Another JaTaHoKu I just made, to prove to myself that it’s possible to make accessible JaTaHoKus. You might want to solve this one before the previous one.

jatahoku1-5twos

Rules Place numbers from 1 to 5 into some empty cells, such that each row, column and region contains each number exactly once. Clues within the grid are Tapa clues; the numbered cells form a valid Tapa solution with respect to these. Clues along the bottom and right edges are skyscraper clues. Clues along the top and left are Japanese Sums clues, with question marks standing in for unspecified digits. (I.e., 10 would be two question marks.)

Puzzle 93: JaTaHoKu

5 Replies

Here’s a first (Ja)TaHoKu, which I made to prepare for the Logic Masters. Mostly an exercise in the interaction between the Tapa rules and the equal number of cells per row/column/region; that part seems to have potential as a Tapa variation. Would you have thought that even without rooms, the one Tapa clue implies that the mirrored cell has to be shaded?

jatahoku1-4

Rules Place numbers from 1 to 4 into some cells, such that each row, column and region contains each number exactly once. Clues within the grid are Tapa clues; the numbered cells form a valid Tapa solution with respect to these. Clues along the bottom and right edges are skyscraper clues.

Puzzle 75: Tapa LITS

Leave a reply

The next Tapa Variations Contest is coming up: TVC XVIII. Once again, Bram is kindly sharing a set of practice puzzles (intro, part 1). To give a little bit back, here’s one more Tapa LITS.

One other of the types that will show up is Different Tapa, so solve the one from this blog if you haven’t: Puzzle 70: Different Tapa.

tapa-lits.png

Rules Solve as a standard Tapa. In addition, the shaded cells must form a valid LITS solution (minus the rooms), i.e., the wall consists of tetrominos, and similar tetrominos can’t touch by edge.

Puzzle 74: Tapa knapp-daneben

Leave a reply

To welcome the new year, here’s a Tapa “knapp-daneben”, i.e., all clues are off by one. The type features on Tapa Variations Contest XVII which takes place on the week-end. I’m really looking forward to that! For a more thorough preparation, check the practice puzzles on Bram’s blog. tapa-kd

Rules Increase or decrease each digit by one, then solve as a regular Tapa. Digits may become zero, even multiple, but not negative.