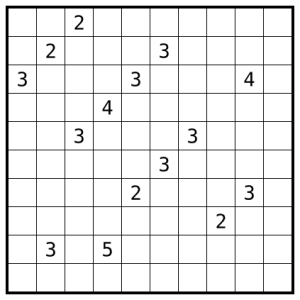
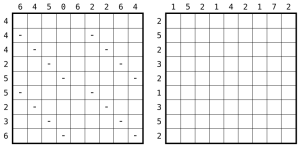
The German qualification is through. The puzzles will be available there again sooner or later, maybe I’ll post my contribution to the set here later. Here’s a somewhat trickier Checkered Fillomino that didn’t make it. I’m not sure it’s right to tag it as hard, that depends a lot on how well you know the type. 
The online qualification tournament for this year’s German Logic Masters is taking place next weekend, authored by Silke Berendes and me. It’s open as a contest to everybody. Let us know on the forum if anything’s unclear in the instruction booklet (the English version hasn’t been proof-read extensively).
Here’s a Double Back puzzle that didn’t make the cut.
One more Lakes puzzle. Enjoy!
EDIT Some more of this type, thanks to EKBM and Zoltán: http://inabapuzzle.com/honkaku/paintp.pdf (by Inaba Naoki), http://5mp.eu/fajlok/logikairejtveny/tavak.372.380_www.5mp.eu_.pdf
Some more Slovak Sums, see the previous one for the rules. This one is certainly more difficult.
Here’s a practice puzzle for the other non-standard type on the Serbian GP this weekend, “Slitherlink Out-Liars” as they call it. I’m not too sure this one is representative of the type; certainly it feels different than the others I’ve solved.
Rules Draw a single loop that doesn’t touch or cross itself by connecting dots horizontally and vertically. Clues inside the loop indicate the number of adjacent edges used by the loop. Clues outside the loop indicate the number of adjacent edges used by the loop, plus or minus 1. Or see the instruction booklet.
Some more puzzles: 2010 German qualification. On croco puzzle: 2013-12-21, 2014-02-08, 2014-04-26. There was also one in the 2014 WPC.
Here’s a practice puzzle I made in London. It took me a while to get it typeset.
Rules Place some walls along grid lines to form a non-branching labyrinth leading from start to finish and visiting every cell. Clues indicate the lengths of all walls ocurring in that row/column. Questionmarks stand for any positive integer.
In other words, draw a path from S to F that travels horizontally and vertically between cell centres, visits every cell, and doesn’t cross itself, then draw walls along every edge that isn’t crossed by the path. The number of question marks outside a row/column is the number of walls of any length in that row/column. Unclued rows/columns can have any number of walls.
You can find better rules and an example in the WPC instruction booklet.
Here’s another fractional skyscrapers puzzle. Numbers 1-7. Edit: flipped, prettier this way.
An update, finally. I’ve been busy starting a new job. This is a split pentomino placement puzzle, as seen in this year’s puzzle GP, a candidate puzzle for the GP finals which were held today during the WPC in London.
Rules Place a full set of pentominos across both grids, such that they don’t touch, not even diagonally. Clues count the number of cells that are part of pentominos in the corresponding row or column.
Last of the set. This is a type that really benefitted from preparation, it takes some getting used to. The contest puzzle ended up going mostly smoothly, unfortunately I ended up spending a lot of time resolving a non-contradiction in one part of the puzzle.
Rules Shade some cells to leave an orthogonally connected set of cells (the “cave”) that doesn’t enclose any shaded cells. All clues must be within the cave. Then draw a path through the cave that travels horizontally or vertically between cell centres that visits all unclued cave cells and doesn’t touch or intersect itself. This path passes through some (at least one) consecutive clues in ascending order, starting at 1 and going straight through any clue. The clue 1 is in the second cell of the path, the highest clue as in the second-to-last cell of the path. The remaining clues are usual cave clues: they count the total number of cave cells that can be seen in horizontal or vertical direction from that cell, including the cell itself.
See the puzzle wiki for German rules (that allow the usual Bahnhof crossings) with an example.
Maybe Puzzles 